15-2강. 최소비용신장트리 (Minimum Spanning Tree) (2)

최소비용신장트리 (Minimum Spanning Tree)

 

 

• Kruskal의 알고리즘

- 에지들을 가중치의 오름차순으로 정렬한다.

- 에지들을 그 순서대로 하나씩 선택해 간다.

   단, 이미 선택된 에지들과 사이클(cycle)을 형성하면 선택하지 않는다.

- n-1개의 에지가 선택되면 종료한다.

 

 

Kruskal의 알고리즘 1

Kruskal의 알고리즘 2

Kruskal의 알고리즘 3

 

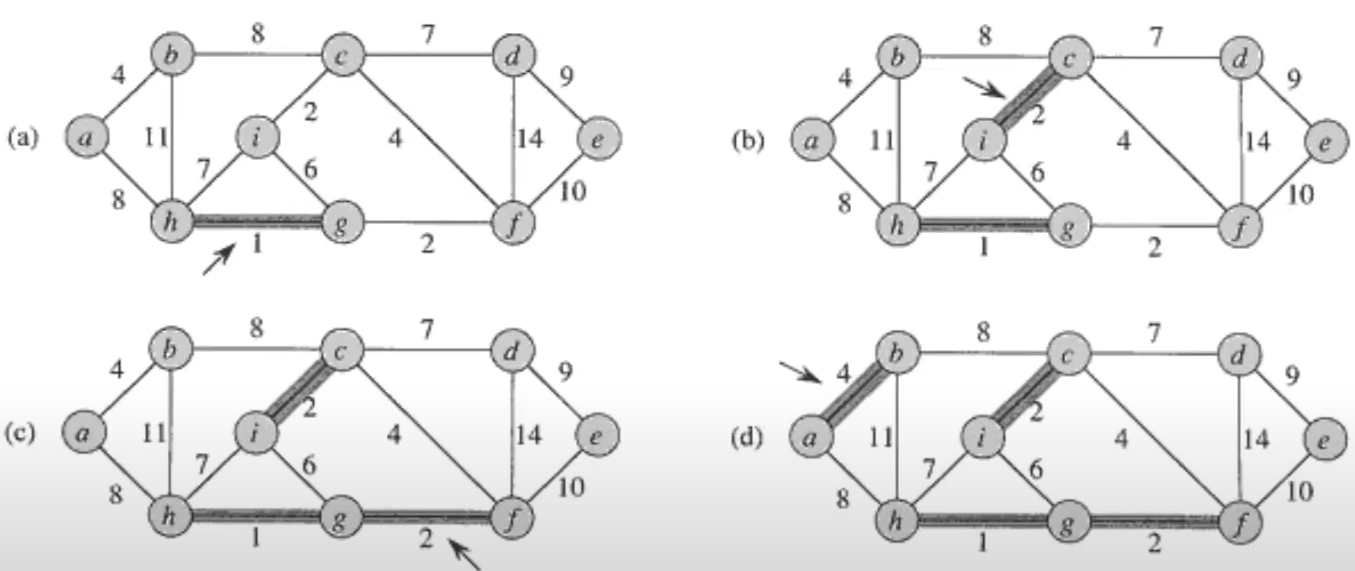
위의 그래프에서, 모른 에지들을 작은 것부터 큰 것 순으로 정렬해 두었다고 가정하자.

(a) : 가장 가중치(weight)가 작은 에지(1)를 선택한다. => 내가 선택한 에지들은 cycle을 형성하지 않는다. (왜? 에지가 하나밖에 선택되지 않았으니까)

(b) : 그 다음으로 가중치(weight)가 작은 에지(2)를 선택한다. => cycle을 형성하지 않는다.

(c) : 그 다음으로 가중치(weight)가 작은 에지(2)를 선택한다. => cycle을 형성하지 않는다.

(b나 c 중에서 어느것이 먼저가 되어도 상관 없다.)

... 반복

(e) : 그 다음으로 가중치(weight)가 작은 에지(6)를 선택한다. => cycle을 형성한다. => 이 에지는 선택하지 않고 버린다.

.. 그 다음으로 가중치가 작은 에지 동시에 cycle을 형성하지 않는 에지를 선택한다. (반복)

 

이제 이 아래 그래프에서

 

Kruskal의 알고리즘 4

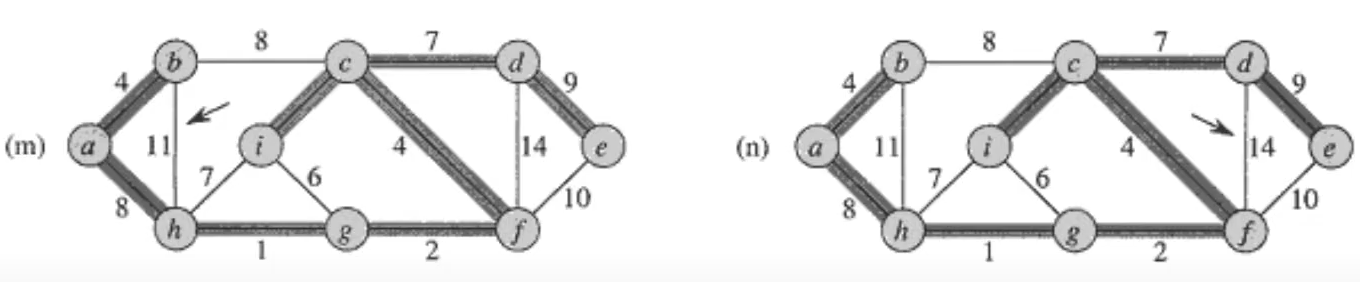
(m)과 (n) 과정은 할 필요가 없다는 것을 알 수 있다. (cycle을 형성하기 때문에!)

 

 

 

• 왜 위의 방법으로 MST(Minimum Spanning Tree : 최소비용신장트리)가 찾아지는가?

- Kruskal 의 알고리즘의 임의의 한 단계를 생각해 보자.

- A를 현재까지 알고리즘이 선택한 에지의 집합이라고 하고, A를 포함하는 MST가 존재한다고 가정하자.

(아래의 그래프에서는 빨강색으로 표시한 에지들을 A라고 가정하자)

 

파랑 뭉탱이와 초록 뭉탱이는 빨간 에지에 의해 연결되지 않았음

 

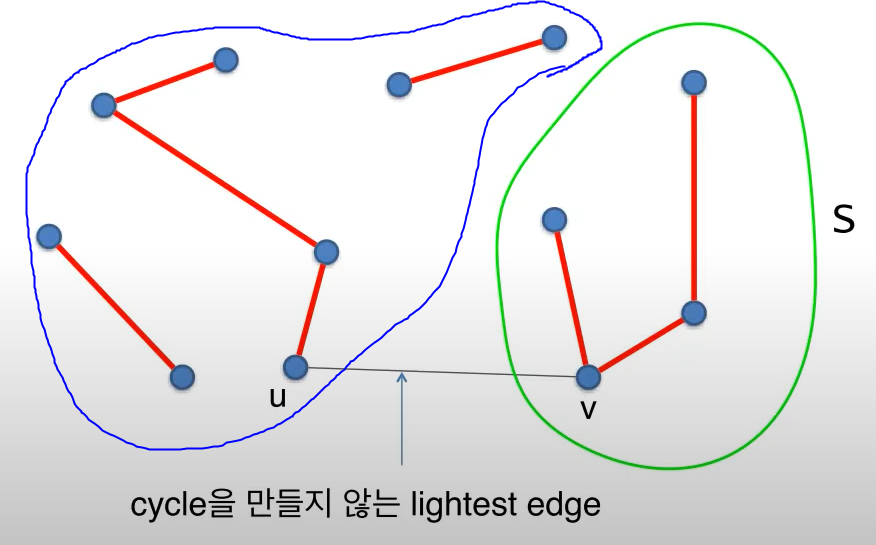
A를 포함하는 MST가 존재한다고 가정해 보자.

파랑 뭉탱이와 초록 뭉탱이를 cross하는 빨간 에지가 생긴다 해도 cycle은 생성되지 않는다. => MST의 후보이다.

+ cycle을 형성하지 않는 lightest edge => Kruskal의 알고리즘에 의한 MST 찾기

 

 

 

• 사이클 검사

- 초기 상태 : 선택된 에지 없음

- 각각의 연결 요소를 하나의 집합으로 표현

 

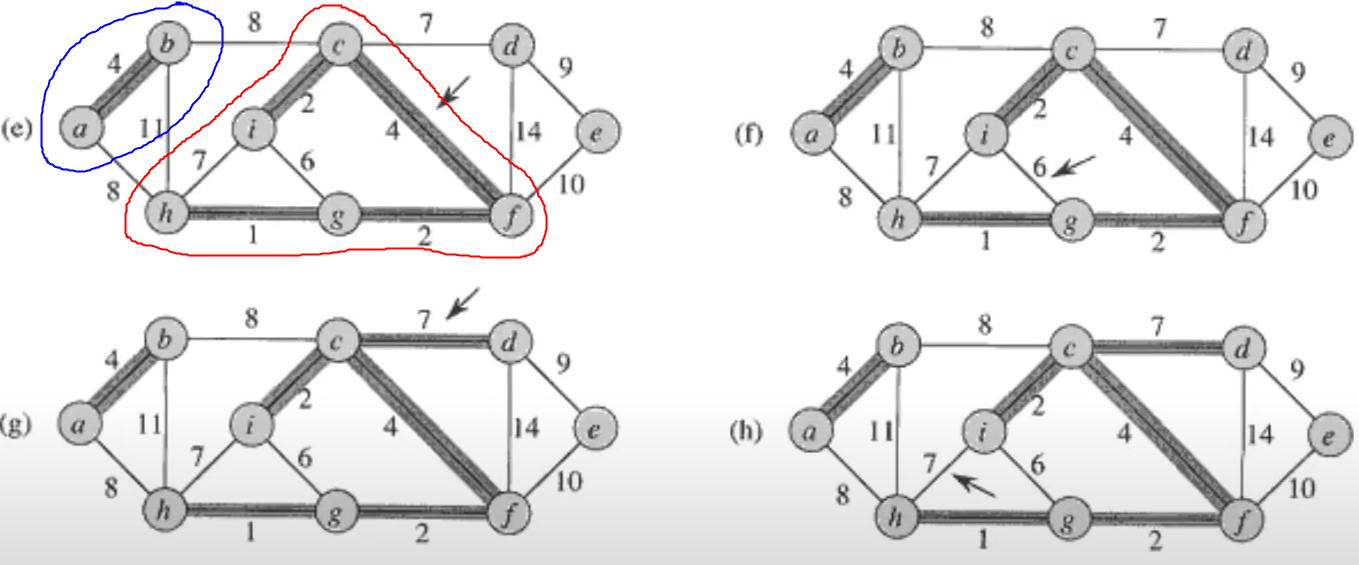
예를 들어 위의 그래프 (e)를 보자.

{a, b}, {c, e, i, g, h, f}, {d}, {e} 와 같이 집합으로 표현할 수 있다.

이제 집합 {c, e, i, g, h, f} 안에서 에지가 연결되면 사이클이 형성되고,

집합 {a, b} 중 원소 하나와 집합 {c, e, i, g, h, f} 안의 원소 하나가 연결되면 사이클이 형성되지 않는 것이다.

 

 

Kruskal's Algorithm : 사이클 검사 방법의 초기 상태

 

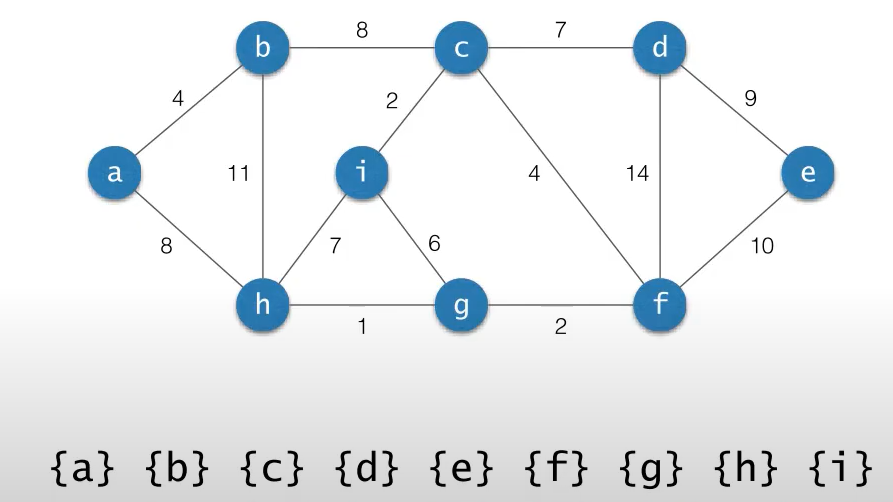
가장 작은 weight의 노드를 찾으면 1인데, 이는 노드 g와 노드 h는 다른 집합에 속했으므로 {g, h}를 만든다.

... 반복

 

 

MST-KRUSKAL(G, w) : 
{
	A <- ø
    for each vertex v ∈ V[G]	// 각각의 노드들을 유일한 원소로 가지는 집합들을 만들어라
    	do MAKE-SET(v)
    sort the edges of E into nondecreasing order by weight w
    for each edgit(u, v) ∈ E, taken in nondecreasing order by weight
    	do if FIND-SET(u) != FIND-SET(v)	// FIND-SET(v) : 노드 v가 속한 집합을 찾아라
        	then A <- A ∪ {(u, v)}
            	UNION(u, v)	// u와 v가 속한 두 집합을 하나로 합친다.
    return A
}

 

 

 

www.inflearn.com/course/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B0%95%EC%A2%8C/lecture/4110?tab=curriculum

영리한 프로그래밍을 위한 알고리즘 강좌 - 인프런